Un coût de transaction toujours plus lourd
Que l’image se fasse à travers le procès kafkaïen ou les 12 travaux d’Astérix, le justiciable qui cherche à contracter afin de valoriser ses droits de propriété intellectuelle est soumis au même fardeau : le coût de transaction. On peut diviser son essence en plusieurs parties : négociation, exécution, protection du droit intellectuel et spécificités des conditions.
Il sera question d’apprécier et d’étayer les différentes difficultés qui s’offrent à celui qui cherche à passer par le contrat. D’autres analyses permettront de comprendre si les nouvelles technologies seront en mesure de faire disparaitre ces inconvénients.
Prémisses :
Le coût total ![]() est fonction de plusieurs variables :
est fonction de plusieurs variables :
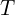 : le coût de négociation
: le coût de négociation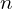 : nombre de parties impliquées
: nombre de parties impliquées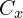 : complexité contractuelle (nombre de clauses spécifiques)
: complexité contractuelle (nombre de clauses spécifiques)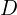 : durée de l’accord (en années ou mois)
: durée de l’accord (en années ou mois)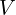 : valeur de l’actif intellectuel
: valeur de l’actif intellectuel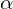 : coefficient lié à la protection de la PI
: coefficient lié à la protection de la PI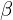 : coefficient lié à la spécificité contractuelle
: coefficient lié à la spécificité contractuelle
L’équation de base est la suivante :
![]()
Dérivation du coût de négociation
Le coût de négociation, noté ![]() , est directement proportionnel au nombre de parties
, est directement proportionnel au nombre de parties ![]() et à la complexité
et à la complexité ![]() . Cependant, pour rendre l’analyse plus précise, on peut introduire un coefficient
. Cependant, pour rendre l’analyse plus précise, on peut introduire un coefficient ![]() , qui modélise l’efficacité de la négociation en fonction du nombre de parties.
, qui modélise l’efficacité de la négociation en fonction du nombre de parties.
Ainsi, le coût de négociation devient :
![]()
avec ![]() étant un coefficient dépendant du type d’accord, par exemple
étant un coefficient dépendant du type d’accord, par exemple ![]() .
.
Dérivation du coût d’exécution
Le coût d’exécution ![]() dépend non seulement de la durée
dépend non seulement de la durée ![]() du contrat, mais aussi d’un facteur d’efficacité
du contrat, mais aussi d’un facteur d’efficacité ![]() , qui tient compte de la longueur et de la complexité de la mise en œuvre dans le temps.
, qui tient compte de la longueur et de la complexité de la mise en œuvre dans le temps.
Ainsi, le coût d’exécution devient :
![]()
Le coefficient ![]() modélise l’influence du temps sur le coût d’exécution et peut varier en fonction de la capacité des parties à s’exécuter rapidement.
modélise l’influence du temps sur le coût d’exécution et peut varier en fonction de la capacité des parties à s’exécuter rapidement.
Dérivation du coût de protection
Le coût de protection ![]() peut être affecté par plusieurs facteurs comme la valeur de la PI
peut être affecté par plusieurs facteurs comme la valeur de la PI ![]() et le niveau de protection juridique
et le niveau de protection juridique ![]() . Le coefficient
. Le coefficient ![]() varie selon le type de propriété intellectuelle (brevet, droit d’auteur, marque), mais on introduit ici un coefficient
varie selon le type de propriété intellectuelle (brevet, droit d’auteur, marque), mais on introduit ici un coefficient ![]() pour tenir compte du niveau de protection requis.
pour tenir compte du niveau de protection requis.
Nous avons donc :
![]()
Le coefficient ![]() représente l’effort nécessaire pour maintenir la protection (par exemple, un brevet dans un domaine technologique peut nécessiter plus de protection qu’une marque déposée).
représente l’effort nécessaire pour maintenir la protection (par exemple, un brevet dans un domaine technologique peut nécessiter plus de protection qu’une marque déposée).
Dérivation du coût de spécificité contractuelle
La spécificité contractuelle ![]() dépend de la complexité des clauses
dépend de la complexité des clauses ![]() , mais nous pouvons aussi introduire un facteur de précision
, mais nous pouvons aussi introduire un facteur de précision ![]() , qui mesure à quel point les clauses sont strictes ou vagues. Une plus grande spécificité entraîne des coûts supplémentaires de gestion et de surveillance des obligations.
, qui mesure à quel point les clauses sont strictes ou vagues. Une plus grande spécificité entraîne des coûts supplémentaires de gestion et de surveillance des obligations.
Ainsi, le coût de spécificité devient :
![]()
Le coefficient ![]() peut être influencé par des facteurs comme le besoin de surveillance continue des clauses ou la nécessité d’ajustements réguliers.
peut être influencé par des facteurs comme le besoin de surveillance continue des clauses ou la nécessité d’ajustements réguliers.
Coût total de transaction raffiné
En intégrant ces éléments, l’équation complète du coût de transaction ![]() devient :
devient :
![]()
Approfondissement des coûts individuels
- Coût de négociation raffiné :
Le coût de négociation peut être influencé par d’autres variables telles que le temps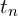 nécessaire pour chaque cycle de négociation. En intégrant cette variable, le coût devient :
nécessaire pour chaque cycle de négociation. En intégrant cette variable, le coût devient :
![]()
On peut introduire un facteur de retard ![]() , qui augmente les coûts en cas de prolongation des négociations :
, qui augmente les coûts en cas de prolongation des négociations :
![]()
Coût d’exécution raffiné :
Le coût d’exécution peut également inclure des ajustements réguliers ![]() , liés à la complexité de la PI ou aux contraintes du marché. Cela donne :
, liés à la complexité de la PI ou aux contraintes du marché. Cela donne :
![]()
Le facteur ![]() représente les révisions contractuelles nécessaires ou les adaptations à des changements imprévus (réglementations, nouvelles technologies).
représente les révisions contractuelles nécessaires ou les adaptations à des changements imprévus (réglementations, nouvelles technologies).
Coût de protection raffiné :
Pour le coût de protection, on peut aussi introduire un terme ![]() , qui mesure l’intensité des attaques potentielles (comme le piratage, la contrefaçon). Cela modifie l’équation de la façon suivante :
, qui mesure l’intensité des attaques potentielles (comme le piratage, la contrefaçon). Cela modifie l’équation de la façon suivante :
![]()
Coût de spécificité contractuelle raffiné :
Le coût lié à la spécificité contractuelle peut inclure un terme ![]() , qui modélise l’effort additionnel nécessaire pour ajuster des clauses trop rigides ou mal définies :
, qui modélise l’effort additionnel nécessaire pour ajuster des clauses trop rigides ou mal définies :
![]()
En intégrant tous ces éléments, le coût total de transaction peut être exprimé de manière très détaillée comme suit :
![]()
Plusieurs constats s’offrent à nous. D’abord, la modélisation complète du coût de transaction peut être toujours plus étayée. Pour autant, la théorie n’est parfois pas très loin de la réalité et la négociation peut, par exemple, toujours être plus approfondie. Il existe toujours plus de facteurs permettant de faire varier plus ou moins fortement ce coût, propres au domaine des contrats. Pire, la propriété intellectuelle bénéficie d’une friction contractuelle liée à la protection du titulaire, ce qui tend à faire augmenter ce coût.